PpHd (./22) :
Surtout que dans mes souvenirs cette équivalence n'est bonne que pour des nombres très grands (genre 1 000 000)

Ben en fait c'est vraiment pas un calcul très compliqué :
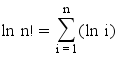
et comme la fonction logarithme est strictement croissante, la somme des valeurs aux points entiers est inférieure à l'intégrale de la fonction entre 1 et n + 1 (en fait cette somme peut être vue comme l'intégrale d'une fonction par paliers qui est toujours en-dessous de la fonction logarithme, c'est évident sur un dessin), et elle est supérieure à l'intégrale de la fonction entre 1 et n (pareil mais en décalant d'un cran et sachant que ln 1 = 0).

Or
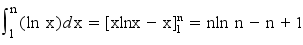
donc nln n est bien un équivalent mais si on veut une bonne approximation il vaut mieux prendre nln n - n + 1, évidemment ^^ (et là l'erreur est inférieure à ln (n+1)).
Par contre quand on veut un O on s'en fout complètement du terme en n, bien sûr.