try Le 13/10/2008 à 11:13 salut est-ce que vous pouvez m'aider pour cet exercice surtout pour le premier
On considère la fonction f définie par :
f(x)= (2x+2)/(x²+2x-3)
On nomme C sa courbe représentative dans le repère orthonormé (O ; vec{i} , vec{j})
1. Etudier la continuité de la fonction f.
2. Montrer que I (-1; 0) est le centre de symétri de C.
3. Déterminer les limites de la fonction aux bornes de son ensemble de définition.
4. Etablir le tableau de variation de la fonction f.
5. En déduire alors d'apès le tableau précédent, suivant les valeurs du paramètre réel m, le nombre et le signe des solutions de l'équation f(x)=m.
6. Retrouver ce résultat en résolvant par l'algèbre l'équation du second dégré mx² + 2(m-1)x - (3m+2)=0
Pour la 1. je sais que l'ensemble de définition est R privé de 1 mais je ne sais pas avec quelle valeur, je dois étudier la continuité.
squalyl Le 13/10/2008 à 11:25Edité par squalyl le 13/10/2008 à 11:28 toutes. Pour chaque valeur v, t'étudies la limite de f(x) quand x tend vers v, et tu montres qu'elle est pas infinie.
le numérateur est un polynome donc par règles de composition il est continu, et tu le divises par un polynome. ha. ben si tu montres que le dénominateur s'annule jamais , ben t'auras jamais de "1/0" donc la fonction sera continue. sinon bah c'est un peu plus fin.
je sais pas en quelle classe t'es mais tout ça c'est quasiment des questions de cours, lis le déja.
try Le 13/10/2008 à 11:27 salut pour ça je dois utiliser la forme conjugué ?
rah mais étudie ton cours!
t'as trouvé l'ensemble de def: R privé de 1. Bah f est continue sur R privé de 1, étudie les limites en 1 pour savoir comment ça s'y comporte: est ce que ça diverge ou est ce que ça reste près de la même valeur?
L'ensemble de définition est déjà faux. Un polynôme de degré 2 à coefficients réels qui a une racine réelle en a forcément 2, qui sont forcément distinctes si le polynôme n'est pas de la forme a(x-x0)², et ce polynôme n'est clairement pas de cette forme (x²+2x-3 n'est pas multiple constant de (x-1)²=x²-2x+1). Et la deuxième racine ne peut pas non plus être racine du numérateur: la racine unique de 2x-2 est x1=-1 qui n'est pas racine de x²+2x-3. Donc il y a forcément 2 "pôles" (endroits à asymptote verticale où la fonction n'est pas définie parce qu'elle diverge vers + ou - l'infini des 2 côtés) et la fonction est continue partout ailleurs.
try Le 15/10/2008 à 00:13 Pour le 2)
je dois utiliser cette formule f(a+h) + f(a-h)= f(-1+3) + f(-1-3)= f(2) + f(-4) après comment je fais pour savoir s'il est symétrique ?
Sburb Le 15/10/2008 à 01:09 Pourquoi h=3 ???
Relis ton cours, mais je ne pense pas que ça soit la formule qui soit marquée.
Tu dois montrer que f(-1+x)+f(-1-x)=2*0=0 pour tout x de l'ensemble de définition
try Le 15/10/2008 à 16:46 est-ce que tu peux m'aider pour le 4) parce que moi j'ai trouvé de -infini à -3 c'est croissant de -3 à 1 c'est décroissant et de 1 à -infini c'est croissant.
try Le 15/10/2008 à 17:45 ok merci est ce que tu peux m'aider pour la 5)
oui je sais mais j'ai un peu de mal avec les gens qui font aucun effort manifeste pour chercher.
c'est un forum d'aide ou de donnage de solutions sans réfléchir?
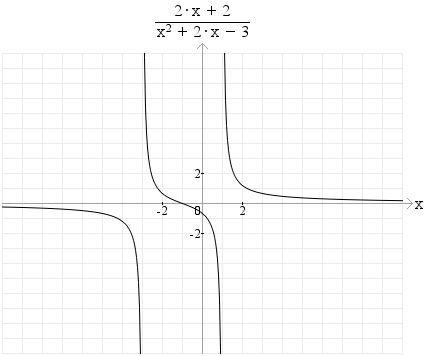
) centrale de la courbe: que vaut f(0) et que peux-tu en déduire pour le signe des solutions x de f(x)=m? C'est pourtant tout bête...)
