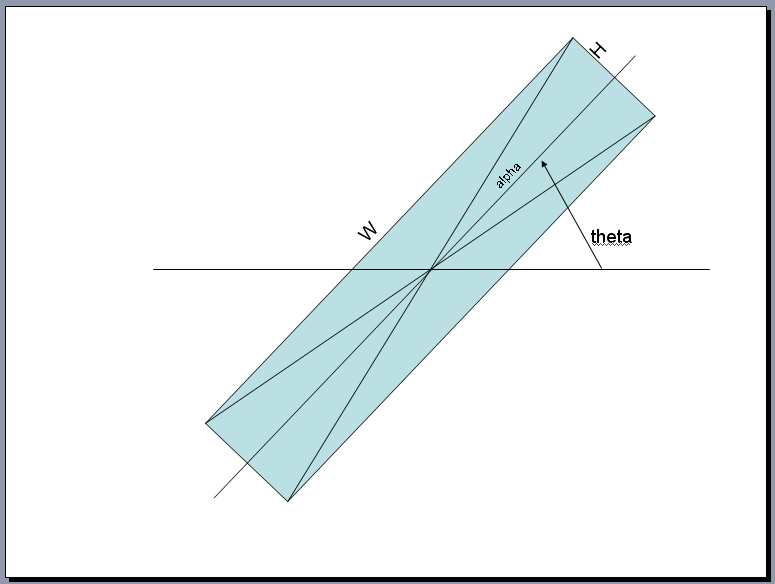
tu pars du anchor (centre)
les 4 coins sont à une demi-hypothénuse du centre
radius = 0.5 * sqrt(width*width+height*height)
après tu connais l'angle theta, zéro quand le rectangle est horizontal - plus pratique que si tu te bases sur l'hypothénuse, comme ça tu dépends pas des proportions du rectangle.
tu calcules en plus l'angle que forme un coté du rectangle avec son hypothénuse
alpha = arctan2 ( height/2, width/2) = arctan2 (height, width) (théorème de thalès)
ça marche aussi si tu inverses height et width, ça fera juste un rectangle tourné de 90 degrés.
maintenant tu connais donc les angles qui visent les 4 sommets à partir du centre
le premier est à l'angle theta + alpha
le 2eme " " " theta - alpha
le 3eme " " " theta + alpha + 180 = symétrie centrale du premier
le 4eme " " " theta - alpha + 180 = symétrie centrale du 2eme
pour rotater un point A à partir du centre C tu fais
XA = XC + radius * cos(angle)
YA = YC + radius * sin(angle)
C'est l'équation d'un cercle.
tu peux faire "sioux" si tu sais que cos(angle+180) = -cos(angle) et que sin(angle+180)= -sin (angle) ou que les points sont symétriques par rapport au centre.
tu connais XC,YC (anchor) radius et les 4 angles, WIN.
du coup pourquoi t'as besoin d'une bounding box? tu peux utiliser une bounding box pivotée, cad que tu compares les coordonnées des 4 points de ton rectangle pour voir si elles sont dans le mur, pas besoin de min max, ce sera faux.






 (Dommage qu'il ne soit pas sorti en Europe (à ma connaissance))
(Dommage qu'il ne soit pas sorti en Europe (à ma connaissance))
