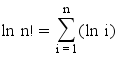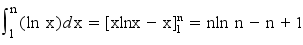Trier 4 éléments. - Page 1

Question simple : comment trier 4 éléments avec le moins de comparaison possible ?
Je n'arrive pas à faire mieux que 6 comparaisons.

      if (CMP (0, 1) > 0)
	SWAP (0 ,1);
      if (CMP (2, 3) > 0)
	SWAP (2, 3);
      if (CMP (1, 2) <= 0)
	return;
      if (CMP (0, 2) <= 0) {
	SWAP (1, 2);
        if (CMP (2, 3) > 0)
          SWAP (2, 3);
      } else if (CMP (0, 3) <= 0) {
        ROLL (2, 1, 0);
        if (CMP (2, 3) > 0)
          SWAP (2, 3);
      } else {
        SWAP (0, 2);
        SWAP (1, 3);
      }

Des idées ?

prende le plus petit de a et b dans a et le plus grand dans b
prende le plus petit de a et c dans a et le plus grand dans c
prende le plus petit de a et d dans a et le plus grand dans d

prende le plus petit de b et c dans b et le plus grand dans c
prende le plus petit de b et d dans b et le plus grand dans d

prende le plus petit de c et d dans c et le plus grand dans d

tu ne peux pas faire moins il me semble => 6 comparaisons également

un tri comptage serait adapté? (pas de comparaisons)
http://fr.wikipedia.org/wiki/Tri_comptage

./3: Je ne vois pas comment ca pourrait être plus rapide que 6 comparaisons. Ca n'est intéressant qu'à partir d'un grand nombre à trier.

y'avait pas marqué le plus rapide

ben si il demande moins de 6 comparaisons, c'est que c'est une question de rapidité...

surtout qu'il n'a pas précisé quels types de donné il veut trier : ca peut être des entiers, des float, des string, ou n'importe quel objet avec une fonction de comparaison... donc il faut un algo qui ne tient pas compte du type

Si a, b, c et d sont les 4 éléments à trier.

Permuter a et b au besoin pour que a<b (I)

De même pour que c<d (II)

De même permuter au besoin a et c pour que a<c (III)

De même pour que b<d (IV)

A ce stade, on sait que a est le plus petit élément et d le plus grand.

Reste à permuter éventuellement b et c pour que b<c. (V)



Ca fait 5 comparaisons et on ne peut pas faire mieux et on peut le démontrer mais flemme.

Quoique, on ne peut pas faire mieux que 5 au pire, mais on peut faire mieux en moyenne :

- Classer a<b

- Classer c<d

- Comparer a et c (on a donc trois éléments classés : a<c<d ou c<a<b)

- Insérer le dernier élément dans les trois éléments classés (ça se fait en une ou deux comparaisons)


Donc 4 ou 5 comparaisons.

Je savais bien que c'était possible de faire mieux
Merci hippo

Faut toujours s'attendre pour la solution optimale à trouver log(n!)
(n le nombre d'éléments à trier ; logarithme en base 2)

Le pseudo-code:

      if (CMP (0, 1) > 0)
	SWAP (0 ,1);
      if (CMP (2, 3) > 0)
	SWAP (2, 3);
      if (CMP (0, 2) > 0) {
	SWAP (0, 2);
        SWAP (1, 3);
      }
      if (CMP (1, 2) <= 0)
        return;
      if (CMP (1, 3) > 0)
        ROLL (1, 2, 3);
      else
        SWAP (1, 2);

Tiens, moi j'appellerais qsort.

Hippopotame (./10) :
Faut toujours s'attendre pour la solution optimale à trouver log(n!)
(n le nombre d'éléments à trier ; logarithme en base 2)

Pourquoi ? D'ailleurs je croyais que c'était n*ln(n)

Hippopotame (./7) :
Si a, b, c et d sont les 4 éléments à trier.

Permuter a et b au besoin pour que a<b (I)

De même pour que c<d (II)

De même permuter au besoin a et c pour que a<c (III)

De même pour que b<d (IV)

A ce stade, on sait que a est le plus petit élément et d le plus grand.

Reste à permuter éventuellement b et c pour que b<c. (V)


Ca fait 5 comparaisons et on ne peut pas faire mieux et on peut le démontrer mais flemme.

Application à 4 éléments du tri fusion, si je ne m'abuse .

Sasume (./13) :

Hippopotame (./10) :
Faut toujours s'attendre pour la solution optimale à trouver log(n!)(n le nombre d'éléments à trier ; logarithme en base 2)

Pourquoi ? D'ailleurs je croyais que c'était n*ln(n)

Moi aussi je dirais plutôt que c'est en N*log₂(N)...

Oui mais n.log2(n) n'est pas le premier terme du développement limité de log2(n!) lorsque n tend vers l'infini ?

*Ressort sa formule de Stirling.*
log₂(n!) ~ log₂(sqrt(2*pi*n)*(n/e)^n) = n*log₂(n) - n/ln(2) + log₂(n)/2 + log₂(sqrt(2*pi))
Ah oui, tiens, n*log₂(n) est le terme prépondérant de log₂(n!), je n'en savais absolument rien...

Par contre, parler de développement limité avec n tendant vers l'infini (sans avoir de 1/n), j'ai comme un petit doute ...

Sasume (./13) :
Pourquoi ? D'ailleurs je croyais que c'était n*ln(n)

Il y a n! permutations de n éléments.
En x comparaisons on peut distinguer 2^x telles permutations.

Il faut donc que 2^x >= n!

Donc x>= log2(n!)

C'est la limite exacte, ensuite on simplifie en O(nlog(n)) puisque de toute façon les algorithmes pour trier de grands tableaux ne donneront cette complexité optimale qu'à une constante prêt...

Cool, il me restait au moins ce DL dans la tête après les cours de physique statistique de cette année

Ethaniel (./16) :
Par contre, parler de développement limité avec n tendant vers l'infini (sans avoir de 1/n), j'ai comme un petit doute .

Si si Plus n est grand, plus les deux expressions convergent vers la même valeur On ce sert de cette équivalence pour calculer log(n!) en un temps raisonnable et en utilisant une mémoire raisonnable.
Le calcul d'une factorielle prend un temps et une mémoire gigantesque avec des nombres pourtant raisonnables (ex : n=100). Et puis, après, pour faire un log sur un nombre de 3 millions de chiffres, bonjour !

On s'en sert en physique statistique par exemple, par contre je ne sais plus pourquoi

Le calcul d'une factorielle prend un temps et une mémoire gigantesque avec des nombres pourtant raisonnables (ex : n=100).

MDR. Calculer 100000! me prend juste une seconde sur mon pentium M à 1.7 GHz (de manière exacte). Et ce n'est même pas l'algo le plus efficace pour le cacluler.

Thibaut (./18) :
Et puis, après, pour faire un log sur un nombre de 3 millions de chiffres, bonjour !

Aucun problème. J'ai déjà calculé avec des flottants de 1 000 000 000 de bits (mais pas sur mon portable, c'est vrai )

PpHd (./19) :
MDR. Calculer 100000! me prend juste une seconde sur mon pentium M à 1.7 GHz (de manière exacte). Et ce n'est même pas l'algo le plus efficace pour le cacluler.

Heu, moi je ne suis pas MDR mon cher. Parceque si tu es dans un programme de simulation d'un phénomène physique, par exemple, ben 1 seconde multiplié par 100.000 simulations, sachant qu'il y'a ensuite le logarthime à calculer derrière, et qu'il y a d'autres calculs à faire à côté, ça en ferait du temps Je ne comprends pas pourquoi tu ne vois pas l'intérêt de l'équivalence de la formule pour les grands nombres.

Les physiciens se servent très souvent d'équivalences pour simplifier leurs calculs. On a passé l'année à faire ça, dans toutes les matières (électrostatique, magnétisme, thermodynamique statistique, etc). Ca permet d'obtenir des formules approchées (sous des hypothèses précises), qui évitent de traîner des tonnes termes, aboutir à des formules à rallonge, hyper compliquées, qui ne donneraient qu'un résultat trop peu meilleur

./17 > Zouli !

./18 > Il me semblait que l'on ne parlait de DL que pour les écritures de la forme f(x) = a + b*x + c*x² + d*x³ + ... + o(xⁿ) avec x~0, mais c'est loiiiiiiin pour moi, je dois confondre avec je ne sais quoi.

Thibaut (./20) :
Heu, moi je ne suis pas MDR mon cher. Parceque si tu es dans un programme de simulation d'un phénomène physique, par exemple, ben 1 seconde multiplié par 100.000 simulations, sachant qu'il y'a ensuite le logarthime à calculer derrière, et qu'il y a d'autres calculs à faire à côté, ça en ferait du temps Je ne comprends pas pourquoi tu ne vois pas l'intérêt de l'équivalence de la formule pour les grands nombres.

Ah. Je connais pas beaucoup de simulation physique faisant intervenir log(n!) (Remarque peut être en stat).
Surtout que dans mes souvenirs cette équivalence n'est bonne que pour des nombres très grands (genre 1 000 000).
Mettons quand même. Mais 1s reste pour moi un temps raisonnable pour calculer 100000!
De toute facon, dans une telle simulation j'aurais précalculé tous les log(n!) pour tous les n qui sont suceptibles d'arriver (même jusqu'à 100000, ca prendra pas trop de place).

Thibaut (./20) :
Les physiciens se servent très souvent d'équivalences pour simplifier leurs calculs. On a passé l'année à faire ça, dans toutes les matières (électrostatique, magnétisme, thermodynamique statistique, etc). Ca permet d'obtenir des formules approchées (sous des hypothèses précises), qui évitent de traîner des tonnes termes, aboutir à des formules à rallonge, hyper compliquées, qui ne donneraient qu'un résultat trop peu meilleur

L'important est de maitriser l'erreur commise. Après tu peux faire ce que tu veux.

Mais 1s reste pour moi un temps raisonnable pour calculer 100000!

OK. Quant au physicien chercheur, il dira qu'il ne peut pas bosser avec la formule de base. Pour simuler X particules, ça lui ferait plus de X secondes de calcul (faut rajouter les autres opérations à côté) Et sans les équivalences certains systèmes physiques seraient impossibles à mettre en équation, car les calculs seraient insolubles

Ah. Je connais pas beaucoup de simulation physique faisant intervenir log(n!) (Remarque peut être en stat).

Je parlais des équivalences en général. On fait énormément de simplifications par équivalences en physique. (1+f(x))^(1/2) est un autre exemple, qui sert pour certains problèmes d'optique ondulatoire et d'électrostatique (et je ne suis qu'en L2, je ne peux parler que de l'aperçu que j'ai eu jusqu'ici).

PS : plus concrètement, ça permet aussi d'appliquer les formules sur des données réelles avec une simple calculatrice, sans sortir l'artillerie lourde (PC + logiciels qui vont bien)

Ethaniel (./16) :
Par contre, parler de développement limité avec n tendant vers l'infini (sans avoir de 1/n), j'ai comme un petit doute .

Oui tu as raison en fait. Je confonds DL et équivalences

PpHd (./22) :
Surtout que dans mes souvenirs cette équivalence n'est bonne que pour des nombres très grands (genre 1 000 000)

Ben en fait c'est vraiment pas un calcul très compliqué :
et comme la fonction logarithme est strictement croissante, la somme des valeurs aux points entiers est inférieure à l'intégrale de la fonction entre 1 et n + 1 (en fait cette somme peut être vue comme l'intégrale d'une fonction par paliers qui est toujours en-dessous de la fonction logarithme, c'est évident sur un dessin), et elle est supérieure à l'intégrale de la fonction entre 1 et n (pareil mais en décalant d'un cran et sachant que ln 1 = 0).

Or
donc nln n est bien un équivalent mais si on veut une bonne approximation il vaut mieux prendre nln n - n + 1, évidemment ^^ (et là l'erreur est inférieure à ln (n+1)).
Par contre quand on veut un O on s'en fout complètement du terme en n, bien sûr.

D'ailleurs, si on veut un gagner un ordre dans la précision, il faut prendre exactement le milieu de cet intervalle d'erreur (donc nln(n)-n+1 + ln(n+1)/2 ), là c'est vraiment très précis parce que le reste du développement asymptotique est O(1) (en O(1/n) si on arrange la constante correctement).

Plus précisément :

J'adore ces développements fumeux

(J'ai modifié PrettyPrint pour avoir .)

./26 > Cf. ./16 avec la formule de Stirling .

Au fait, tu la démontres comment, la formule de Stirling ?
Thepro > merci

27> Et la suite du développement?